Formule van Hooghoudt
De formule van Hooghoudt (1940 p.603) geeft de hoeveelheid grondwater die afstroomt uit een gedraineerd perceel.
verklaring symbolen
| q | : | afvoer naar de sloten of drains (m/d) |
| l | : | afstand tussen de sloten aan weerszijden van het perceel (m) |
| m0 | : | maximale opbolling van het grondwater in het midden van het perceel (m) |
| k1 | : | doorlatendheid van de bodem boven het slootpeil (m/d) |
| k2 | : | doorlatendheid van de bodem beneden het slootpeil (m/d) |
| d | : | dikte van de equivalentlaag van Hooghoudt (m) |
| D | : | dikte van het watervoerend pakket onder het slootpeil (m) |
| u | : | natte omtrek van de sloot of drainbuis (m) |
Toepassing
bepalen drainafstand
De formule van Hooghoudt wordt gebruikt om uit te rekenen op welke afstand drainbuizen aangelegd moeten worden om een perceel optimaal te ontwateren.
Daarvoor wordt de formule herschreven (Hooghoudt, 1940 p.632):
Deze vergelijking geeft de vereiste slootafstand L, voor een maatgevende afvoersituatie waarbij een afvoer s moet worden afgevoerd en de opbolling niet groter mag zijn dan een te kiezen kritische waarde m0.
Voor het kiezen van deze waarden zijn tabellen met ontwateringsnormen opgesteld (Cultuurtechnisch Vademecum, 1988 p.526).
equivalentlaag d
De dikte van de equivalentlaag d wordt geschat met (Cultuurtechnisch Vademecum, 1988 p.514):
Het berekenen van de equivalentlaag d met bovenstaande formule is lastig, want de slootafstand L is niet vooraf bekend.
Berekening van de equivalntlaag d vereist enkele iteratieslagen waarbij een slootafstand L wordt aangenomen, d wordt uitgerekend en L wordt berekend met Hooghoudt. De berekende L wordt vervolgens gebruikt om de equivalentlaag d opnieuw te schatten, waarmee weer een slootafstand L wordt berekend die dichter bij de juiste waarde ligt. In de praktijk zijn drie of vier iteraties nodig om op de juiste waarde uit te komen.
Uiteraard is het probleem met software als de Excel solver ook automatisch op te lossen.
Voor het berekenen van de equivalentlaag d zijn naast benaderingsformules ook tabellen beschikbaar (Hooghoudt, 1940 p.656-694; Cultuurtechnisch Vademecum, 1988 p.514).
meer praktische informatie
De formule van Hooghoudt is in het overzicht van formules op deze site te vinden onder het geval ontwatering van een perceel door ondiepe sloten.
De formule van Hooghoudt heeft een eigen pagina op Wikipedia.
Achtergrond
geschiedenis
Volgens Van Hoorn (1992) werd de vergelijking voor volkomen sloten voor het eerst afgeleid door Colding in 1872, vervolgens door Hooghoudt in 1937 en tenslotte door Aronovici en Donnan in 1946.
In de internationale literatuur staat deze vergelijking bekend als de Donnan vergelijking.
De formule voor onvolkomen sloten, met onderscheid tussen grondwaterstoming boven het drainagepeil en daaronder is voor het eerst gepubliceerd door Hooghoudt in 1940 (blz 584).
afleiding
De formule van Hooghoudt is een uitwerking van de klassieke formule voor stroming in een freatisch pakket met neerslag door een peilverschil in twee volkomen kanalen:
Wanneer de peilen links en rechts gelijk zijn kunnen we de opbolling midden tussen beide watergangen definieren als:
Bovenstaande vergelijking voor het verloop van het freatisch vlak wordt:
Invullen van m0 en enig herschrijven geeft:
Waarin we de vergelijking van Hooghoudt herkennen (Cultuurtechnische Vademecum, 1988; blz 513):
gekromde stroombanen
De formule van Hooghoudt was een belangrijke vondst, want hij slaagde erin om het probleem van gekroimde stroombanen nabij een sloot te omzeilen.
Hooghoudt geeft de volgende schematisatie van het ontwateringsvraagstuk (Hooghoudt, 1937 p.522):
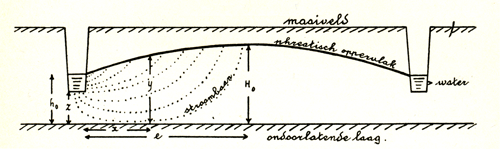
Een perceel wordt ontwaterd door twee sloten. De sloten zijn ondiep, onder de sloten bevindt zich een watervoerende laag van enige dikte. Daardoor krommen de stroombanen van het grondwater naar de slootbodem. Het grootste deel van het afstromende grondwater gaat door de slootbodem.
De kromming van stroombanen geeft weerstand, wat leidt tot extra opbolling van de grondwaterstand. Het vraagstuk is alleen exact op te lossen in twee dimensies, wat leidt tot ingewikkelde formules die in de praktijk niet handig werken (Hooghoudt, 1940).
equivalentlaag van Hooghoudt
Hooghoudt vereenvoudigt het probleem tot een eendimensionaal rekenschema waarvoor een eenvoudige formule is af te leiden.
Hij doet dat door onderscheid te maken in grondwaterstroming bóven het niveau van de slootbodem en ónder de slootbodem.
De radiale weerstand wordt verrekend door de dikte D van de doorstroomde laag onder de slootbodems te reduceren tot de equivalantdikte d. Dit geeft extra weerstand, zonder dat een tweedimensionaal rekenschema nodig is.
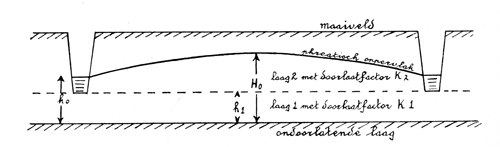
Bijkomend voordeel is dat gerekend kan worden met een doorlatendheid k1 van de ondergrond en een doorlatendheid k2 van de bovengrond.
Dat is bijvoorbeeld handig voor pleistocene zandgronden, waar veelal een dun pakket fijnzandig lemig dekzand (k2) boven een dik pakket grofzandige leemarme rivierzanden ligt (k1).
Referenties
Hooghoudt, S.B. (1937). Bijdragen tot de kennis van eenige natuurkundige grootheden van den grond. No. 6. Bepaling van de doorlatendheid in gronden van de tweede soort: theorie en toepassingen van de kwantiatieve strooming van het water in ondiep gelegen grondslagen, vooral in verband met ontwaterings- en infiltratievraagstukken. Bodemkundige instituut te Groningen. Verschenen in de reeks Verslagen van landbouwkundige onderzoekingen No 43(13)B p. 461-676.
Hooghoudt, S.B. (1940). Bijdragen tot de kennis van eenige natuurkundige grootheden van den grond. No. 7. Algemeene beschouwing van het probleem van de detailontwatering en de infiltratie door middel van parallel loopende drains, greppels, slooten en kanalen. Bodemkundige instituut te Groningen. p. 515-707.
Werkgroep Herziening Cultuurtechnisch vademecum, 1988. Cultuurtechnisch vademecum. Vereniging voor landinrichting.