Formule van Mazure
De formule van Mazure geeft hoeveelheid de kwel in een polder achter een dijk met hoog buitenwater.
Formules
stijghoogte
De stijghoogte onder de deklaag wordt beschreven door (Verruijt, 1970):
Deze vergelijking geeft de relatie tussen het peil in het buitenwater h0, het polderpeil hp en de stijghoogte in het grondwater φ.
De formule wordt veel gebruikt om het effect van peilveranderingen op de grondwaterstand te berekenen. Ze wordt vaak aangeduid als de formule van Mazure. In de oorspronkelijke publicatie (Mazure, 1936) komt ze echter niet voor, maar ze is daaruit wel eenvoudig af te leiden.
debiet
Het debiet in het grondwater onder de deklaag wordt gegeven door de vergelijking die bekend staat als de formule van Mazure (Verruijt, 1970):
kwelbezwaar
De totale hoeveelheid kwel naar de polder wordt gegeven door het debiet op afstand x=0 (Verruijt, 1970):
Dit is de hoeveelheid kwelwater die met een gemaal moet worden uitgemalen, bovenop de neerslag in de polder.
verklaring symbolen
| q(x) | : | debiet van het grondwater op afstand x (m) |
| φ(x) | : | stijghoogte van het grondwater onder de deklaag op afstand x (m) |
| x | : | afstand tot de rand met een vaste stijghoogte (het buitenwater) (m) |
| ho | : | stijghoogte op x=0 (peil van het buitenwater) (m) |
| hp | : | gemiddelde freatische grondwaterstand in de polder (m) |
| k | : | doorlatendheid van het watervoerend pakket (m²/dag) |
| H | : | dikte van de watervoerende laag (m) |
| λ | : | spreidingslengte (m) |
Toepassing
De formule van Mazure wordt gebruikt om te bepalen hoeveel water moet worden uitgemalen bij verhoging van het buitenwater of verlaging van het polderpeil.
De formule voor de stijghoogte wordt veel gebruikt om een snelle inschatting te maken van het effect van aanpassing van het steefpeil op de omgeving.
toepassingbereik
De formule van Mazure wordt nogal eens toegepast buiten het bereik waarvoor de formule geldig is. Kenmerkend is het exponentieel uitdempen van het effect met toenemende afstand x. Die uitdemping wordt veroorzaakt door de watervoerende sloten in de deklaag, die op een vast peil gehouden worden en daardoor onbeperkt grondwater afvangen of infiltreren.
De praktische consequentie is dat de formule van Mazure alleen mag worden toegepast als er een min of meer regelmatig patroon van sloten aanwezig is. Die sloten moeten watervoerend zijn en een vast peil houden, ongeacht de grootte van de peilverandering.
oneindig grote polder
De polder strekt zich vanaf de dijk uit tot in het oneindige. In de praktijk zijn polders aan alle kanten begrensd door andere polders met een ander streefpeil of door buitenwater. Dat roept de vraag op hoe groot een polder moet zijn om randeffecten uit te kunnen sluiten. Mazure zegt hierover het volgende:
Achtergrond
Wieringermeerrapport
Mazure publiceerde zijn formule in het Aanhangsel van zijn bijdrage aan het rapport over de Wieringermeer (1936).
Hij begint met de algemene oplossing van de stroming onder een deklaag:
Op basis hiervan geeft hij eerst de formule voor het debiet in een polder met een lengte L, die aan weerskanten wordt begrensd door een vast peil. Vervolgens behandelt hij de kwel naar polder die zich vanaf een vaste rand oneindig ver uitstrekt en geeft zijn bekende formule.
Hij gaat er daarbij vanuit dat de dijk een breedte B heeft, waardoor zijn vergelijkingen nog iets uitgebreider zijn dan de bovenstaande formule.
Tenslotte geeft Mazure de vergelijking voor kwel naar een ronde polder omsloten door een vaste rand en hij laat zien hoe deze vergelijking zich verhoudt tot de voorgaande gevallen.
artikel uit 1932
In 1932 publiceerde Mazure een artikel in De Ingenieur over het onderwerp "kwel onder een dijk". Hij introduceert daar de aanname dat de stroming in de deklaag verticaal is.
Voor de stroming in het watervoerend pakket gaat hij nog uit van cirkelvormige stroombanen onder de dijk door. Dat leidt tot lastige oplossingen waarin de elliptische integraal voorkomt (Mazure, 1932).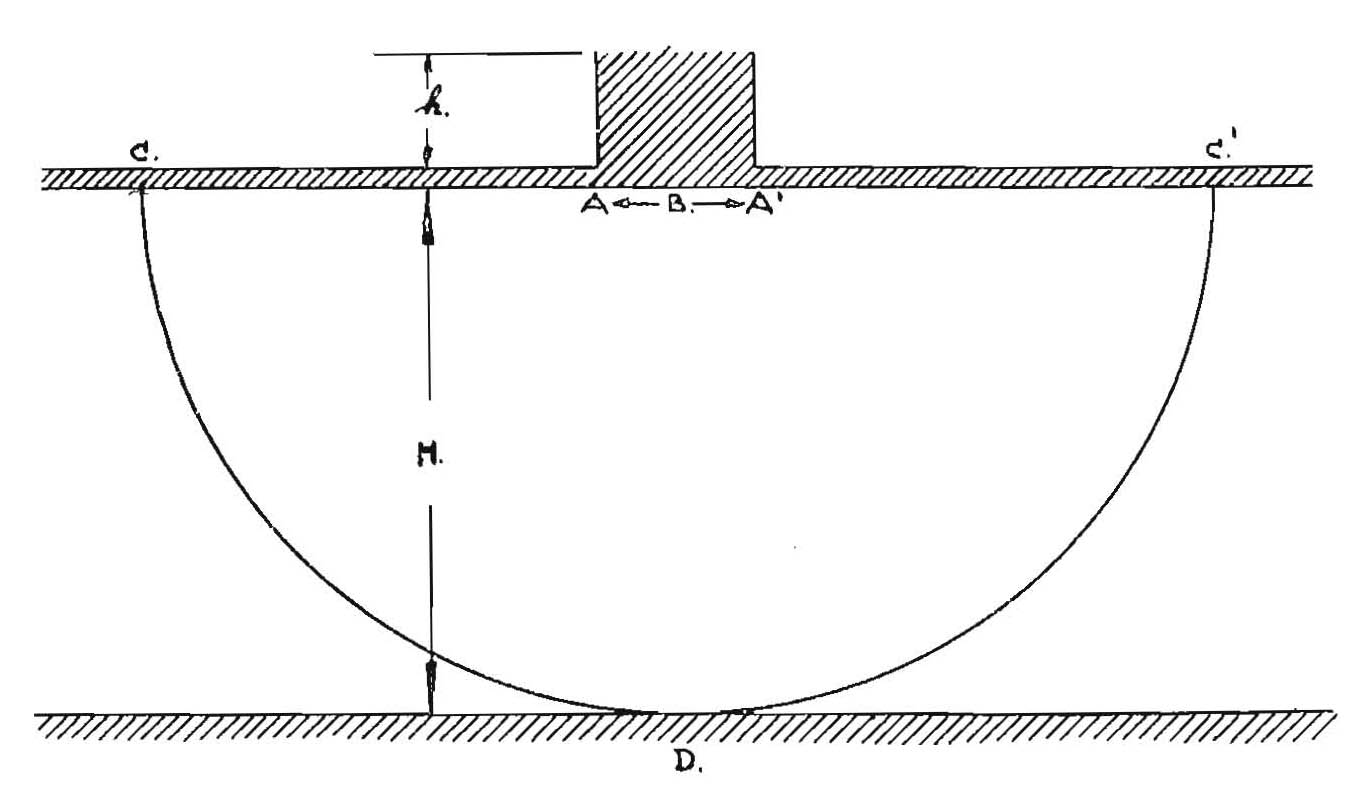 
Bovendien is de kwel bij deze benadering per definitie beperkt tot een afstand H achter de dijk, gelijk aan de dikte van het watervoerend pakket, omdat de grootste stroomcirkel onder de dijk raakt aan de basis van de watervoerende laag.
Een uitgebreidere bespreking van het artikel uit 1932 is opgenomen onder de klassieken.
De opmerkelijke stap in de publicatie uit 1936, is dat Mazure horizontale stroombanen in het watervoerend pakket veronderstelt. Daardoor komt hij uit op de eenvoudige formule met een exponentieel uitdempend verloop.
Referenties
Mazure, J.P. (1932). Invloed van een weinig doorlatende afdekkende laag op de kwel onder een dijk. De Ingenieur, nr 47, B41-B43.
Mazure, J.P. (1936). Kwel en chloor bezwaar in de Wieringermeer. Gepubliceerd als bijlage 10 in: Geohydrologische gesteldheid van de Wieringermeer. Rapport, samengesteld door den dienst der Zuiderzeewerken in samenwerking met het Rijksbureau voor Drinkwatervoorziening. Rapporten en Mededelingen betreffende de Zuiderzeewerken no 5. Algemeene Landsdrukkerij 's Gravenhage
Verruijt, A. (1970). Theory of Groundwater Flow. Macmillan.