Onttrekking in een afgesloten pakket (formule van Theis)
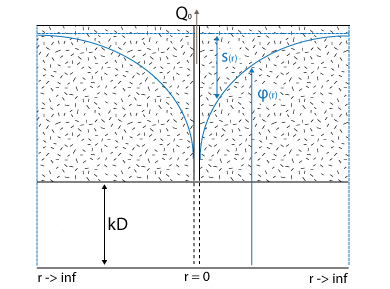
In een afgesloten watervoerende laag wordt grondwater onttrokken aan een put. Er is in de omgeving van de put geen rand met een vaste stijghoogte en de aquifer ontvangt geen water door de boven- of onderrand. Het onttrokken grondwater is volledig afkomstig van toestroming van grondwater uit de aquifer zelf. Daardoor treedt nooit een stationaire situatie op. De verlaging zal in theorie oneindig blijven toenemen.
De instationaire verlaging wordt berekend met de formule van Theis (1935)
De formule van Theis is vooral interessant voor het analyseren van pompproeven. Daarbij is de verlaging korte tijd na het starten van de onttrekking interessant.
Een andere toepassing is het berekenen van de verlaging in een relatief dik freatisch pakket zonder grondwateraanvulling, bijvoorbeeld door een onttrekking ten behoeve van beregening in een droge zomer.
Formules
instationaire verlaging
De verlaging in de tijd wordt berekend met de formule van Theis (Bot, 2011 p.28):
Hierin is W(u²) de well function van Theis (zie onder techniek > hydrologische functies) en u² is gedefinieerd als:
verklaring symbolen
| s(r) | : | verlaging in het watervoerende pakket (m) |
| r | : | afstand tot de put (m) |
| Q0 | : | grootte van de onttrekking uit de put (m3/dag) |
| kD | : | doorlaatvermogen van het watervoerend pakket (m²/dag) |
| S | : | bergingscoëfficient (-) |
| t | : | tijd vanaf het begin van de onttrekking (dagen) |
Rekenvoorbeeld
In een diep watervoerend pakket wordt grondwater onttrokken. De onttrekking Q0 is 1 miljoen m3/jaar. De geohydrologische eigenschappen zijn: doorlaatvermogen kD = 1500 m²/dag, de elastische bergingscoëfficient S = 0.0001.
Bovendstaande grafiek De laat de verlaging zien van de stijghoogte op de tijdstippen t = 10^0, 10^1,...,10^5 (vanaf 1 dag tot ongeveer 273 jaar na het begin van de onttrekking).
toepassingsbereik van de formule van Theis
De grafiek laat zien dat de verlaging die wordt berekend met de formule van Theis oneindig doorgaat, ook na een absurd lange onttrekkingsperiode. Dat komt doordat er geen voedende grens is, niet langs de bovenrand (infiltratie) en niet op een zekere afstand R van de put (een gebied met watervoerende sloten bijvoorbeeld).
De formule van Theis is bedoeld voor berekeningen op vrij korte afstand van de put, niet al te lang na het begin van de onttrekking. Buiten dit bereik is de berekende verlaging onrealistisch en moet een andere formule gebruikt worden, die wel rekening houdt met voeding door neerslag of waterlopen, bijvoorbeeld de formule van Hantush.
rekenvoorbeeld in python
Bijgevoegd python script maakt de grafiek met de verlaging volgens Theis. De waarde van W(u) wordt berekend met de functie ExpInt die standaard beschikbaar is in de module SciPy.
rekenvoorbeeld in Excel
Bijgevoegd excel sheet geeft een rekenvoorbeeld in Excel.
Het blad graphWu geeft een uitwerking van de wel function W(u) met de benadering van Shrivastava. Het blad rekenvoorbeeld geeft de verlaging van een put, waarbij voor de well funtion W(u) een eenvoudige benadering van Huisman (1972) is genomen:
De benadering volgens Huisman is voldoende nauwkeurig voor waarden van u kleiner dan 0,1; kort na de start van de onttrekking op grote afstand van de put zijn de waarden van u groter en is deze benaderingsformule niet toepasbaar.
Referenties
[1] Bot, A.P. 2011. Grondwaterzakboekje. Uitgegeven door Bot Raadgevend Ingenieur. www.grondwaterzakboekje.nl
[2] L. Huisman, 1972. Groundwater Recovery. Macmillan.
[3] C.V. Theis, 1935. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using groundwater storage. Transactions American Geophysical Union Vol. 16: pp.519-524