Onttrekking in een dik freatisch pakket of in een watervoerend pakket onder een kleilaag

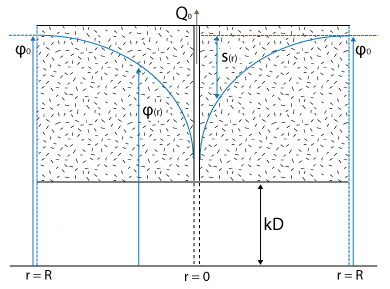
ontrekking-in-afgesloten-pakket

In een watervoerende laag met een constant doorlaatvermogen kD wordt water onttrokken. Op afstand R van de onttrekking ligt een rand met een vaste grondwaterstand. Er is geen voeding van het pakket door de bovenrand, het onttrokken water is volledig afkomstig van de vaste rand op afstand r=R van de put..

Onderstaande formules zijn in theorie van toepassing op een volledig verzadigde watervoerende laag tussen twee ondoorlatende lagen. Toepassing voor een freatisch pakket geeft betrouwbare resultaten zolang verondersteld mag worden dat het doorlaatvermogen kD niet substantieel kleiner wordt door de verlaging van het grondwater rond de onttrekking. In de praktijk geldt een afname van 5% tot maximaal 10% als toelaatbaar.

Voor praktische toepassing van de formule is het van belang de afstand R zorgvuldig te kiezen. Op deze afstand is de verlaging door de onttrekking per definitie gelijk aan nul. In de praktijk is het niet altijd mogelijk om R te bepalen uit gebiedseigenschappen. Kees Maas wijst erop dat de verlaging bij de put voor deze situatie gelijk is aan de formule van de Glee (onttrekking onder een deklaag) als R gelijk wordt genomen aan de spreidingslengte labda.

Formules

grondwaterstand

De stationaire verlaging van de grondwaterstand in een afgesloten watervoerde laag wordt beschreven door de volgende formule (Verruijt, 1970 p36):

$\varphi(r)-\varphi_{0}=\frac{Q_{0}}{2\pi kD}ln\left(\frac{r}{R}\right)$

debiet

Verruijt (1970) wijst erop dat bovenstaande formule voor berekening van φ(r) herschreven kan worden, zodat het onttrokken debiet berekend kan worden uit een gemeten stijghoogte φw in de put (op locatie ) (Verruijt, 1970 p37):

$Q_{0} = 2\pi kD \frac{\left(\varphi_{0}-\varphi_{w}\right)}{ln\left(\frac{R}{r_{w}}\right)}$

Daarbij wordt echter verondersteld dat er geen noemenswaardige weerstand zit tussen het grondwater naast de put en het waterpeil in de put.

reistijd

Het onttrokken water stroomt toe vanaf de vaste rand op r=R. De Vries (1975) geeft de volgende vergelijking voor de reistijd van een waterddeeltje tussen de rand en de put:

$\fn_cm T =\:\frac{\pi n\,D\, R^2}{Q_0}$

Daarbij wordt verondersteld dat de diameter van de put verwaarloosbaar is (de put bevindt zich op r=0).

De reistijd van de rand tot een locatie r op enig afstand van de put, of tot de rand van een put met een grote diameter (zoals een zandwinplas in bedrijf) is te berekenen met:

$t(r) =\:\frac{\pi n\,D}{Q_0}\left(R^2-r^2\right)$

verklaring van symbolen

φ(r)	:	stijghoogte in het watervoerend pakket (m)
φ(r)	:	stijghoogte op de vaste rand (m)
φ(rw)	:	stijghoogte in de put (m)
r	:	afstand tot de put (m)
R	:	afstand van de vaste rand tot de put (m)
rw	:	ligging van de rand van de put (m)
Q0	:	grootte van de onttrekking uit de put (m3/dag)
kD	:	doorlaatvermogen van het watervoerend pakket (m2/dag)
s(r)	:	verlaging in het watervoerend pakket (m)
t(r)	:	reistijd van een waterdeeltje vanaf de rand (jaren)
T	:	reistijd van een waterdeeltje van de rand naar de put (jaren)
n	:	effectieve porositeit van de watervoerende laag (dimensieloos)

Referenties

Bruggeman, G.A., 1999. Analytical solutions of geohydrological problems. Elsevier Science. Amsterdam

De Vries, J.J. (1975). Some Calculation Methods for Determination of the Travel Time of Groundwater. Aqua-Vu Serie A. No. 5: p3-15. Vrije universiteit, Amsterdam.

Huisman, L. (1972). Groundwater Recovery. Macmillan Press, London.

Verruijt, A. (1970). Theory of Groundwater Flow. Macmillan, London.