Werken met matrixformules

De meeste grondwaterformules beschrijven de grondwaterstroming in één watervoerende laag. Interactie met boven- en onderliggende pakketten wordt beschreven door vaste randvoorwaarden. Bijvoorbeeld een vaste stijghoogte onder een scheidende laag met bekende weerstand c, of een constante flux.

Opeenvolging van effectberekeningen

In de praktijk zijn vrijwel altijd meerdere lagen te onderscheiden. Vaak is ook interactie te verwachten: een verlaging in een regionaal watervoerend pakket heeft effect op de freatische laag erboven. Je lost dat op door eerst de verlaging in het regionale pakket te berekenen, zonder rekening te houden met de verandering in de freatische laag. Daarna zoek je een tweede formule die het effect in de freatische laag berekend, gegeven de berekende verandering in het regionale pakket. Het voordeel van deze werkwijze is dat je in iedere stap eenvoudige modellen toepast. Relaties tussen ingreep en effect blijven duidelijk te volgen. Het nadeel is dat je weinig inzicht krijgt in de interactie tussen beide paketten.

Meerlagenoplossingen

Er zijn grondwaterformules beschikbaar waarmee je de grondwaterstand in meerdere watervoerende lagen tegelijk kunt berekenen. De afleiding van deze formules is gebaseerd op matrixtheorie. Voor het gebruik ervan moet je beschikken over software die functies kan toepassen op matrixen, bijvoorbeeld Mathematica of Matlab.

Het praktisch gebruik van Matrixformules in de geohydrologie is uitstekend beschreven in een artikel van Kees Maas en Theo Olstoorn [1]. Zij geven hier voorbeelden voor stroming naar een diepe rivier en onttrekking van grondwater onder een deklaag (Mazure).

In een tweede artikel geeft Theo Olsthoorn een manier om grondwaterstroming te berekenen in een profiel met opeenvolgende secties [3]. Iedere sectie krijgt een eigen polderpeil, in iedere laag kan per sectie een onttrekking opgelegd worden. Het artikel bevat ook een Matlab script (met enkele typefoutjes, helaas). Met deze aanpak is vrijwel ieder denkbaar geohydrologisch dwarsprofiel door te rekenen.

Voorbeeld

In het artikel van Kees Maas en Theo Olsthoorn [1] staat een voorbeeld in Matlab voor infiltratie vanuit een diepe rivier naar meerdere watervoerende pakketten.
Met dezelfde getallen volgt hier een uitwerking in Mathematica.

Als geldt:

$\fn_cm kD=\begin{bmatrix} 100\\ 200\\ 300\\ 400 \end{bmatrix}$ $\fn_cm c=\begin{bmatrix} 500\\ 600\\ 700\\ 800 \end{bmatrix}$ $\fn_cm h=\begin{bmatrix} 1\\ 1\\ 1\\ 1 \end{bmatrix}$

en $\fn_cm x = 500$

Dan wordt de systeemmatrix:

$\fn_cm A=\frac{1}{10.000}\begin{pmatrix} 0.3667 & -0.1667 & 0 & 0 \\ -0.0833 & 0.1548 & -0.0714 & 0\\ 0 & -0.0476 & 0.0893 & -0.0417\\ 0 & 0 & -0.0313 & 0.0313 \end{pmatrix}$

In Mathematica is phi dan met twee commando's te berekenen:

In: sqrtmA = N[MatrixPower[A,1/2]]

Out: [0.0059 - 0.0018 - 0.00026 - 0.00010 - 0.00089 0.0036 - 0.0012 - 0.00027 - 0.000087 - 0.00081 0.0027 - 0.0011 - 0.000025 - 0.00013 - 0.00079 0.0015]

In: phi = (N[MatrixExp[-x sqrtmA].h])

Out: [0.2778550.5272720.672560.735493]

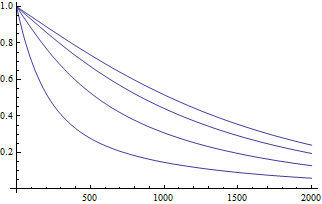
Een grafiek plot je met :

In: Plot[N[MatrixExp[-x sqrtm]. h], {x, 0, 2000}]

Out:

Referenties

[1] H. Haitjema, 2005. The Role of Hand Calculations in Ground Water Flow Modeling. Ground Water. vol. 44, no. 6, pages 786–791

[2] K. Maas en T. Olsthoorn, 1997. Snelle oudjes gaan Matlab. Stromingen jaargang 3 nummer 4 bladzijde 21-42

[3] T. Olsthoorn, 2000. Eendimensionale stroming in meerlagensystemen. Stromingen jaargang 6 nummer 2 bladzijde 13 - 23.